Introduction to package menzerath • menzerath

Introduction

The menzerath package is used to describe fit and plot data following the Menzerath’s law. Menzerath’s law (also known as Menzerath-Altmann law) was initially formulated as a linguistic law describing the relationship between the size of a linguistic construct and its constituents. Consider for example the relationship between the size of a word (y) and its syllables (x). According to Menzerath’s law in its standard formulation the expected relationship should follow:

$y = a \cdot x^b \cdot e^{-cx}$ where a, b and c are parameters of the law.

Installation

The package can be installed from github in R by running the following commands:

install.packages("devtools")
devtools::install_github("sellisd/menzerath", build_vignettes=TRUE)

the build_vignettes=TRUE can be omitted but then the vignettes will not be installed.

Usage

Basic Usage

To demonstrate how to use the package we are going to analyze a classic dataset originally used by Altman 1980 in the mathematical formulation of the Menzerath-Altmann law. The dataset relates the word size, measured in terms of number of syllables to the average syllable size in the word. The size of syllables is measured in terms of number of phonemes.

First we load the library and have a look at the dataset

library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.5
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.4     ✔ tidyr     1.3.1
#> ✔ purrr     1.0.4     
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter()     masks stats::filter()
#> ✖ dplyr::group_rows() masks kableExtra::group_rows()
#> ✖ dplyr::lag()        masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(menzerath)
data(morpheme_syllable)
kbl(morpheme_syllable)

x	y
1	3.10
2	2.53
3	2.29
4	2.12
5	2.09

We can transform the table to a menzerath object and create a plot:

ms <- menzerath(morpheme_syllable)
plot(ms)

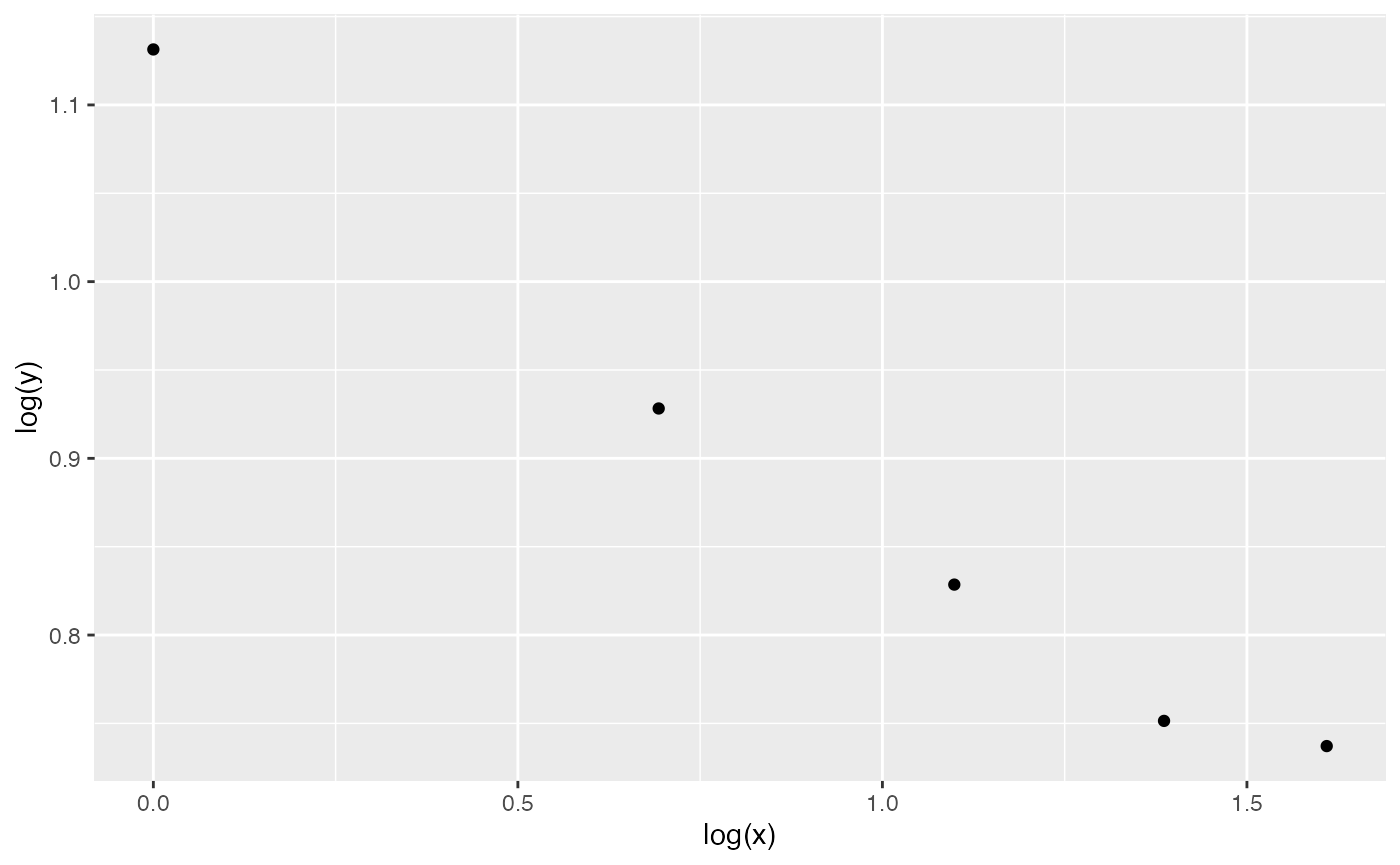
Then estimate the parameters of the law:

fit_menzerath <- fit(ms)
print(fit_menzerath)
#> 
#> Call:
#> lm(formula = log(object$y) ~ log(object$x) + object$x, data = as.data.frame(x = object$x, 
#>     y = object$y, stringsAsFactors = FALSE))
#> 
#> Coefficients:
#>   (Intercept)  log(object$x)       object$x  
#>       1.08529       -0.36854        0.04764

As a linear fit is performed on log scale in order to get the estimated parameters the coefficients have to be transformed. This is facilitated by the get_parameters function:

get_parameters(fit_menzerath)
#> $a
#> [1] 2.9603
#> 
#> $b
#> [1] -0.3685362
#> 
#> $c
#> [1] -0.04764427

The fit can also be visualized with a ribbon plot:

plot(ms, fit=TRUE)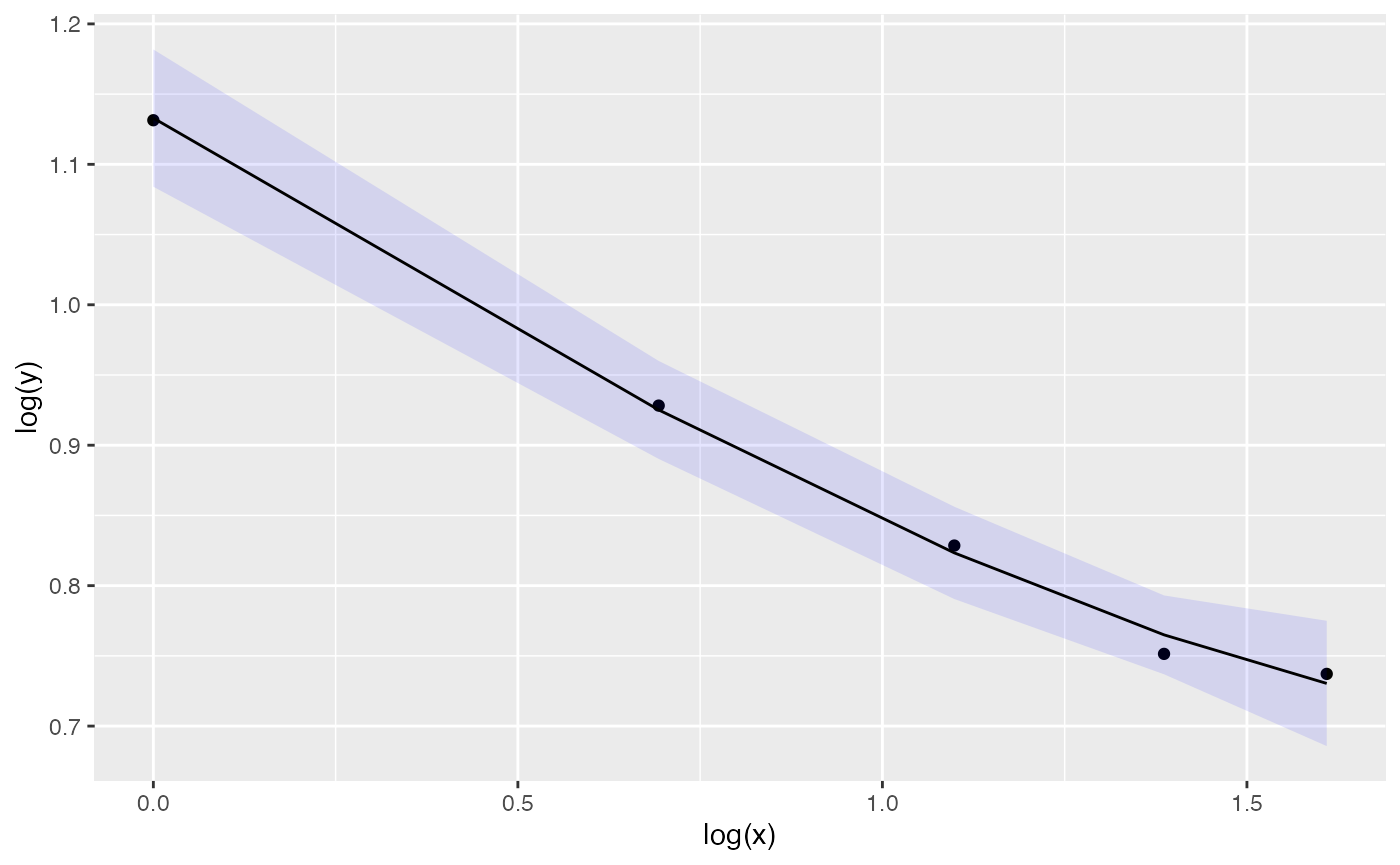

We can now repeat the same analysis in a more recent and larger dataset (Torre et al., 2019). The BG_word_time dataset contains the relationship between the size of breath groups and average word size (in seconds). Breath groups are defined by pauses (e.g. for breathing) during speech.

BG_word_time
#> # A tibble: 45,034 × 2
#>        x     y
#>    <dbl> <dbl>
#>  1     1 0.405
#>  2     1 0.329
#>  3     1 0.146
#>  4     9 0.318
#>  5    10 0.223
#>  6     1 0.442
#>  7     4 0.323
#>  8    11 0.213
#>  9     1 0.261
#> 10     7 0.309
#> # ℹ 45,024 more rows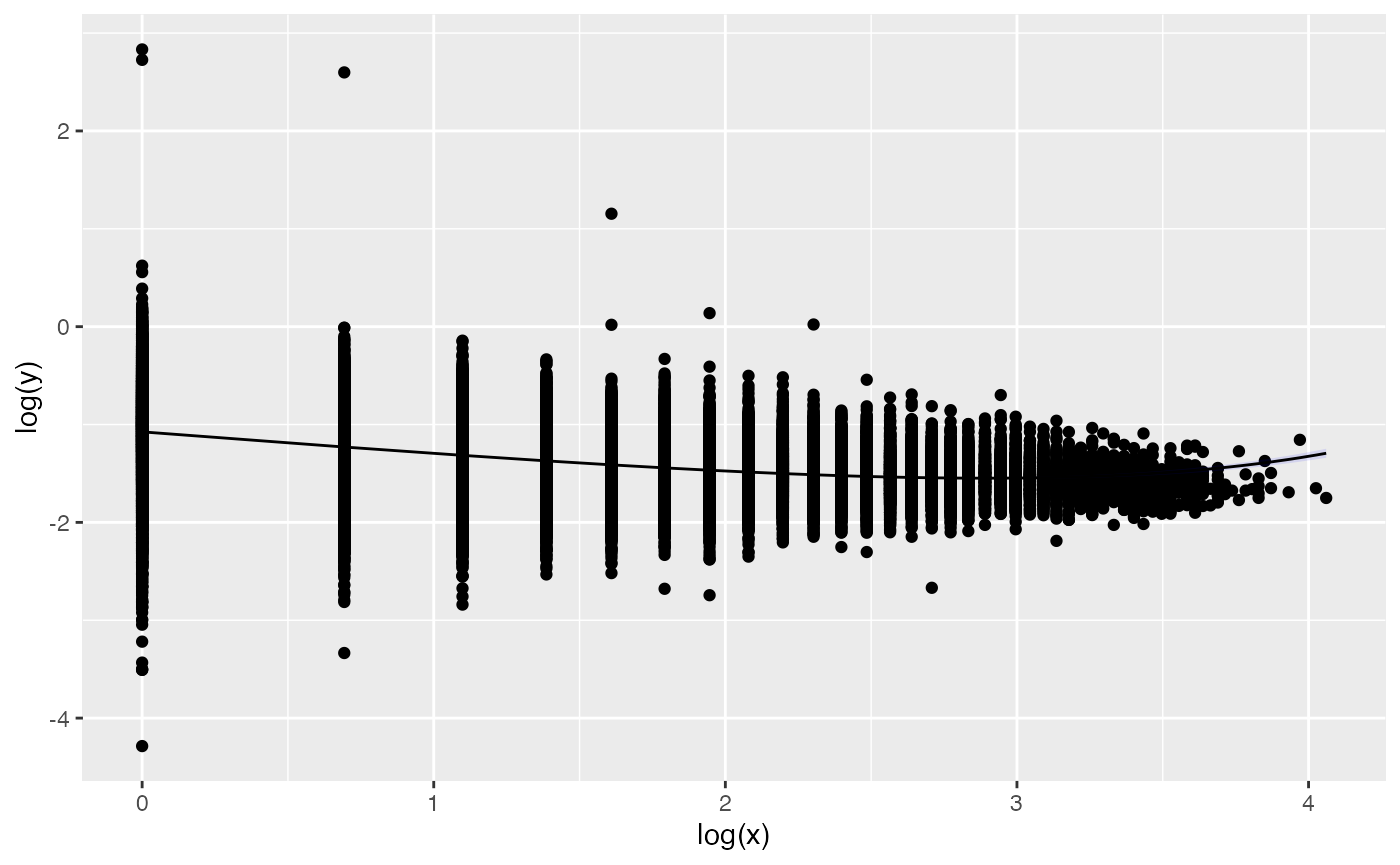

BG_word_time_menzerath = menzerath(BG_word_time)
plot(BG_word_time_menzerath, fit=TRUE)

Alternative models

Different mathematical formulations of Menzerath’s law have been proposed.

method name	equation	parameters	reference
simplified_1	$y = ae^{-cx}$	a, c	Altmann 1980
simplified_2	$y = ax^b$	a, b	Altmann 1980
MAL	$y = ax^be^{-cx}$	a, b, c	Altmann 1980
Milicka_1	$L_{n-1} = a_nL_n^{-b_n}e^{c_nL_n}$	$a_n$ , $b_n$ , $c_n$	Milicka 2014
Milicka_2	$L_{n-1} = a_nL_n^{-b_n}$	$a_n$ , $b_n$	Milicka 2014
Milicka_4	$L_{n-1} = a_n + \frac{b_n}{L_n}$	$a_n$ , $b_n$	Milicka 2014
Milicka_8	$L_{n-1} = a_n + \frac{b_n}{L_n} + \frac{c_n\min(1,L_n-1)}{L_n}$	$a_n$ , $b_n$ , $c_n$	Milicka 2014

Note that methods Milicka_1 and Milicka_2 are identical to the classical Menzerath-Altman formulation (MAL) and simplified_2 correspondingly. The only difference besides notation is the parameter sign so $b=-b_n$ and $c=-c_n$ .

In the classic example of syllable length of Indonesian morphemes Altman estimated a = 2.9603, b = -0.36853 and c = 0.04764. Using the same parameter estimates we can draw the expected form of the law with the different methods.

morpheme_length_vector <- c(1,2,3,4,5)
parameters = c(a=2.9603, b=-0.36853, c=0.04764)
menzerath_methods <- c("simplified_1", "simplified_2", "MAL", "Milicka_1", "Milicka_2", "Milicka_4", "Milicka_8")

mean_syllable_length_vector <- numeric(0)
for(i in c(1:length(menzerath_methods))){
  mean_syllable_length_vector <- c(mean_syllable_length_vector, dmenzerath(morpheme_length_vector,parameters=parameters, method=menzerath_methods[i]))
}
tibble(method = rep(menzerath_methods, times=rep(length(morpheme_length_vector),length(menzerath_methods))),
       morpheme_length = rep(morpheme_length_vector, length(menzerath_methods)),
       mean_syllable_length = mean_syllable_length_vector) %>% 
ggplot(aes(x=morpheme_length, y = mean_syllable_length, color = method)) + geom_line()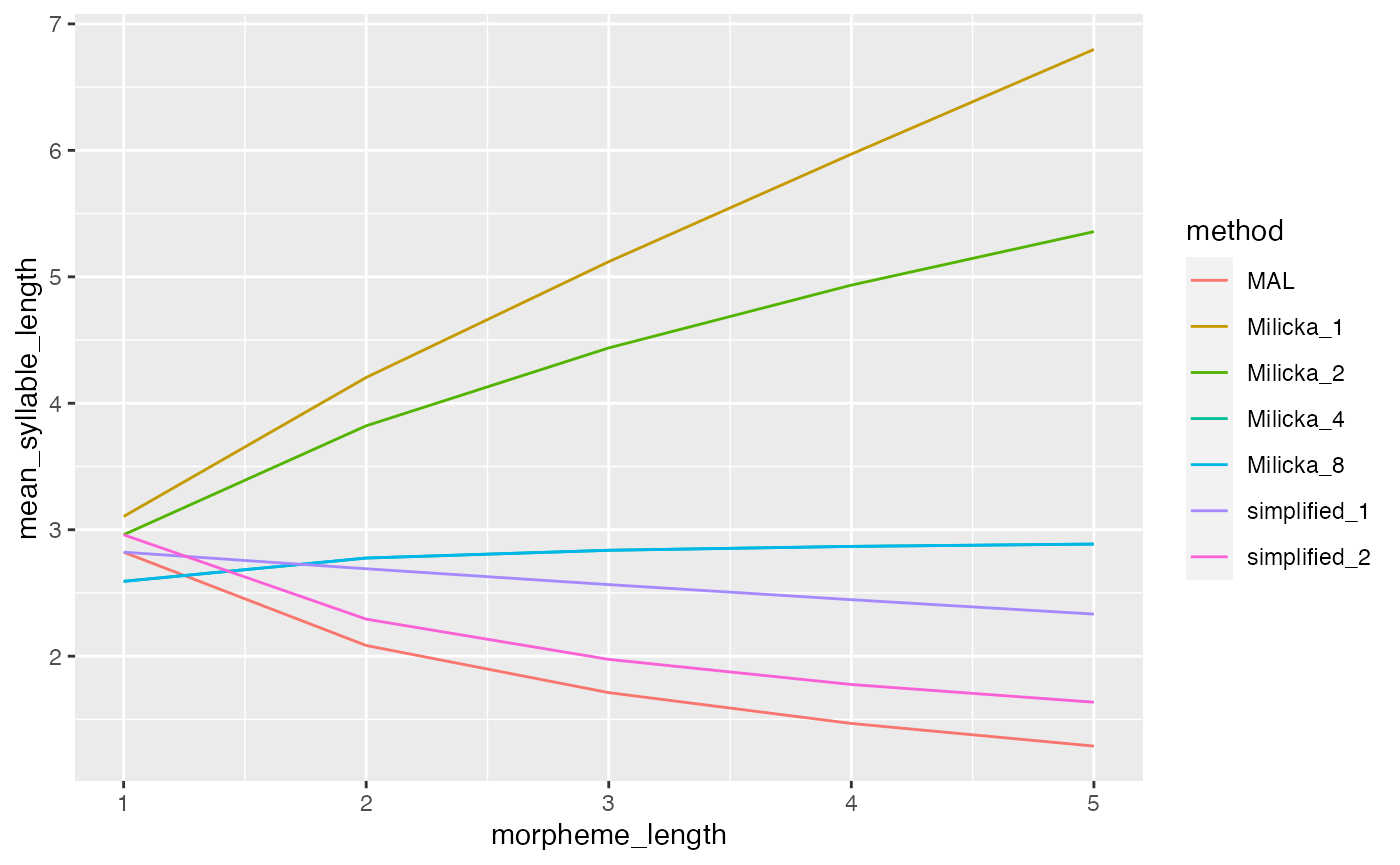

More interesting is to use these alternative models to estimate the parameters from real data. We can do so using Altmann’s data (Altman 1980) on syllable length of indonesian morphemes:

library(cowplot)
#> 
#> Attaching package: 'cowplot'
#> The following object is masked from 'package:lubridate':
#> 
#>     stamp
ms <- menzerath(morpheme_syllable)
MAL_plot <- plot(ms, fit=TRUE, method="MAL") + ggtitle("MAL")
simplified_1_plot <- plot(ms, fit=TRUE, method="simplified_1") + ggtitle("simplified_1")
simplified_2_plot <- plot(ms, fit=TRUE, method="simplified_2") + ggtitle("simplified_2")
Milicka_1_plot <- plot(ms, fit=TRUE, method="Milicka_1") + ggtitle("Milicka_1")
Milicka_2_plot <- plot(ms, fit=TRUE, method="Milicka_2") + ggtitle("Milicka_2")
plot_grid(MAL_plot, simplified_1_plot, simplified_2_plot ,Milicka_1_plot, Milicka_2_plot, ncol = 3)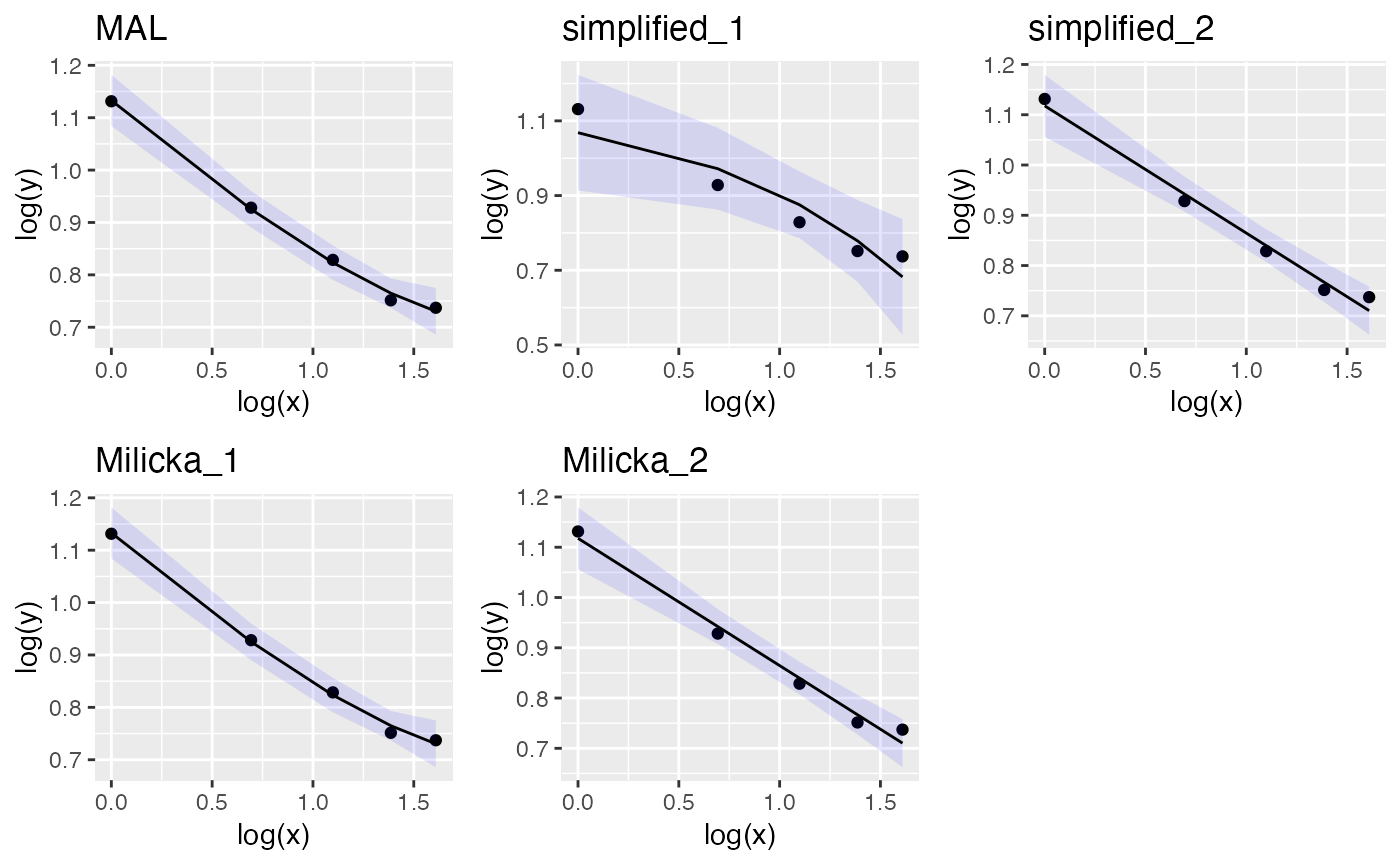

Processing annotated text

We can use the menzerath package to process text that has been manually annotated. Lets assume that we are interested in the levels of clause, word and syllable. To measure Menzerath’s law we manually annotate the text of interest by placing symbols in the end of each construct, constituent and subconstruct. Lets use the following text as an example:

Greece, which is the most beautiful country I know, was the first place we visited in Europe.

We use as delimiters of words a space character (’ ‘), as delimiters of syllables the star character (’*‘) and as delimiters of clauses the plus sign (’+’).

annotated_text <- paste0("Greece* {which* is* the* most* beau*ti*ful* coun*try*",
                         " +I* know* +}was* the* first* place* +we* vi*si*ted* in*",
                         "Eu*ro*pe* +.")
counts_df <- process_text(annotated_text, "+", " ", "*", "{", "}")
kbl(counts_df)

constituents	subconstituents	constructs
6	9	which* is* the* most* beautiful* country +
2	2	I* know* +
5	5	Greece* {was* the* first* place* +
3	8	we* visited* inEurope +

The process_text function calculates the number of constituents and subconstituents per construct, while allowing for the possibility of discontinued constructs (e.g. here a clause that is interrupted by another clause). With this information we can now perform the statistical analyses, first by calculating the average number of subconstituents per construct:

mz <- (counts_df %>%
  mutate(average_subconstituents = subconstituents/constituents))
mz <- menzerath(mz,x="constituents", y = "average_subconstituents")
plot(mz, fit = TRUE)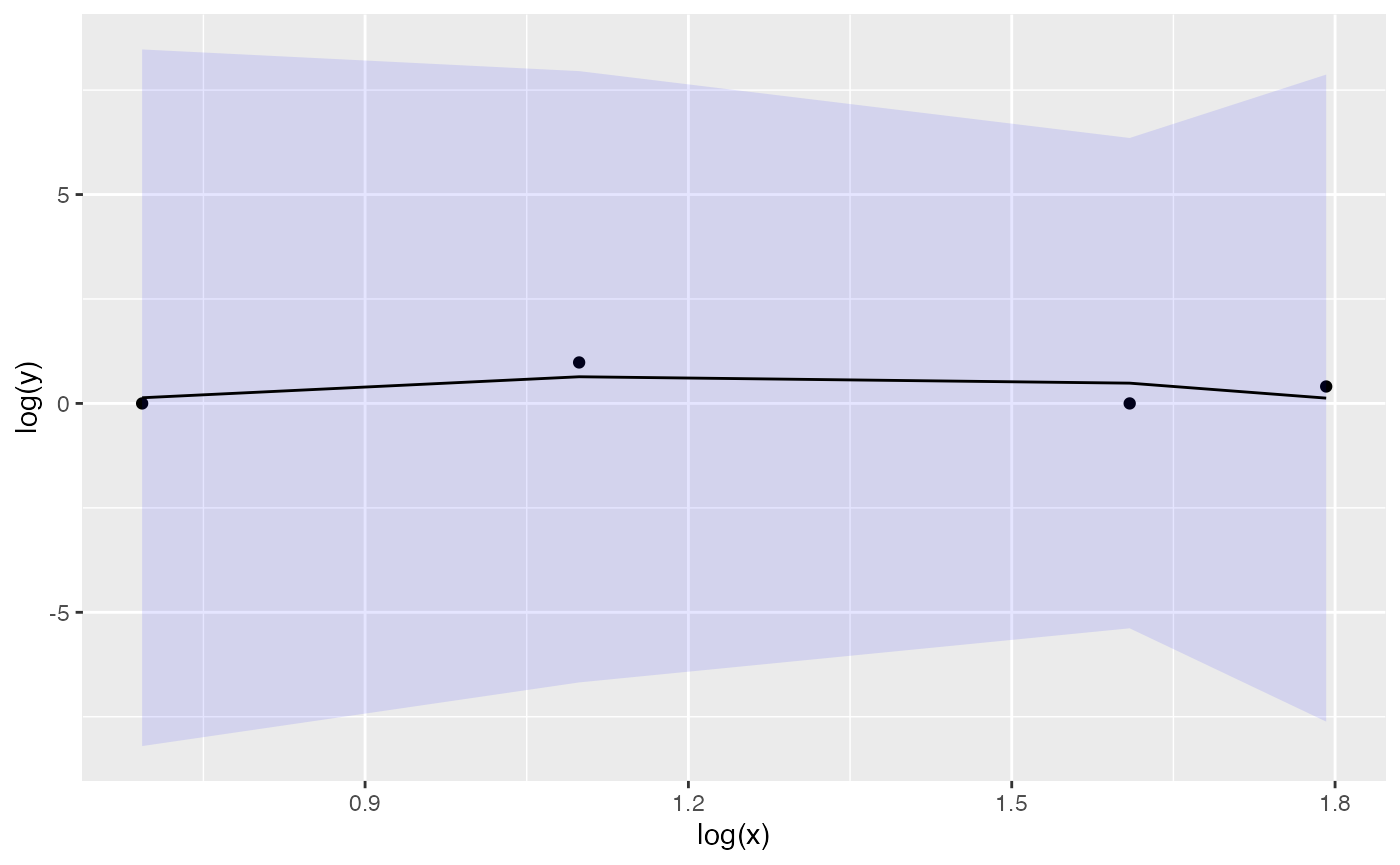

Datasets

In the menzerath package a number of datasets are included in the form of tibbles that can easily be loaded and manipulated to serve as examples or test data. There are some classic datasets from Altmann 1980 and some more recent ones from Torre et al. 2019

Datasets in package

morpheme_syllable: Dataset from Altmann 1980 linking morpheme size and syllable size.
word_syllable_phoneme: Dataset from Altman 1980 on syllable length in English words.
word_syllable_time: Dataset from Altman 1980 on syllable length in Bachka-German words.
BG_word_characters: Dataset from Torre et al. 2019 linking breadth group size and average word size (in number of characters).
BG_word_phonemes: Dataset from Torre et al. 2019 linking breadth group and average word size (in phonemes).
BG_word_time: Dataset from Torre et al. 2019 linking breadth group and word size (in seconds).

Further documentation and details about each dataset can be gained with the help command, e.g:

help(morpheme_syllable)

References

Altmann, G., 1980. Prolegomena to Menzerath’s law. Glottometrika, 2(2), pp.1-10.

Torre Iván G., Luque Bartolo, Lacasa Lucas, Kello Christopher T. and Hernández-Fernández Antoni 2019 On the physical origin of linguistic laws and lognormality in speech R. Soc. open sci.6191023 http://doi.org/10.1098/rsos.191023

Milička, Jiří. (2014). Menzerath’s Law: The Whole is Greater than the Sum of its Parts. Journal of Quantitative Linguistics. 21. 10.1080/09296174.2014.882187.